
For many students, multiplication and especially division leave lasting marks in their mathematical lives. Those who make sense of the concepts deeply and early are primed for lifelong understanding. Studies seeking to identify what math content knowledge is most predictive of students’ long-term learning pinpoint division as one of the most critical concepts to know.
Fundamental to understanding the meaning of multiplication is the concept of an array. This is an arrangement of numbers, objects, pictures (or anything really!) in vertical columns and horizontal rows. In this article, you will learn how to use arrays to show the relationship between multiplication and division.
- Key standard: Use multiplication and division within 100 to solve word problems in situations involving arrays. (Grade 3)
The two ways of thinking about division
Students in Grades 3 and up learn two ways of thinking about division: partitioning and measurement. Students may not use those names at this level, but you can convey their meanings to give students a better understanding of the division process.
Dividing to find the number of objects in each group is called partitioning or “fair sharing.” For example:
A farmer is filling baskets of apples. The farmer has 24 apples and 4 baskets. If she divides them equally, how many apples will she put in each basket?
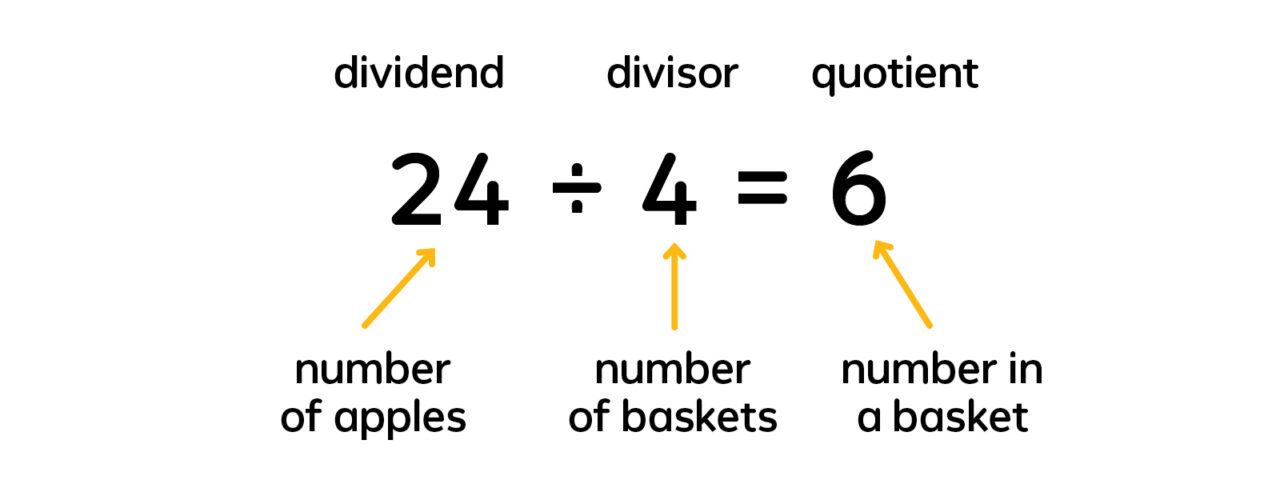
Dividing to find the number of groups is called measuring or repeated subtraction. In the example given, you can think about this as starting at 24 then repeatedly subtracting 4 until you reach 0. Notice that in the equation below, the divisor and quotient switch places, yet the equation remains true.
A farmer has 24 apples. She wants to sell them at 4 apples for $1. How many baskets of 4 can she fill?
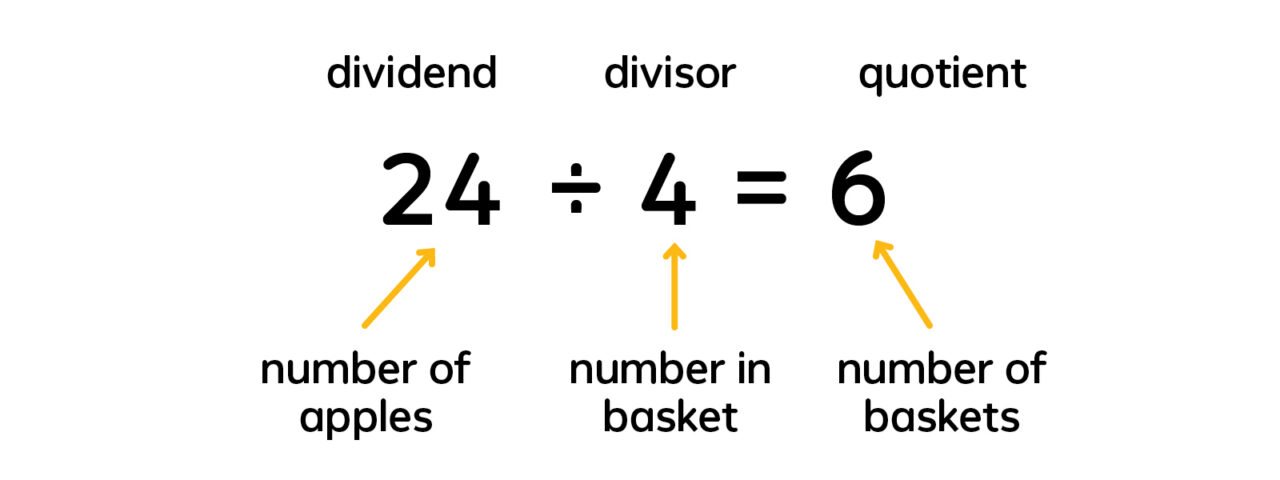
Array division
Manipulatives and visual aids are important when teaching multiplication and division. Students have already used arrays to illustrate the multiplication process, and they can also be used to illustrate division.
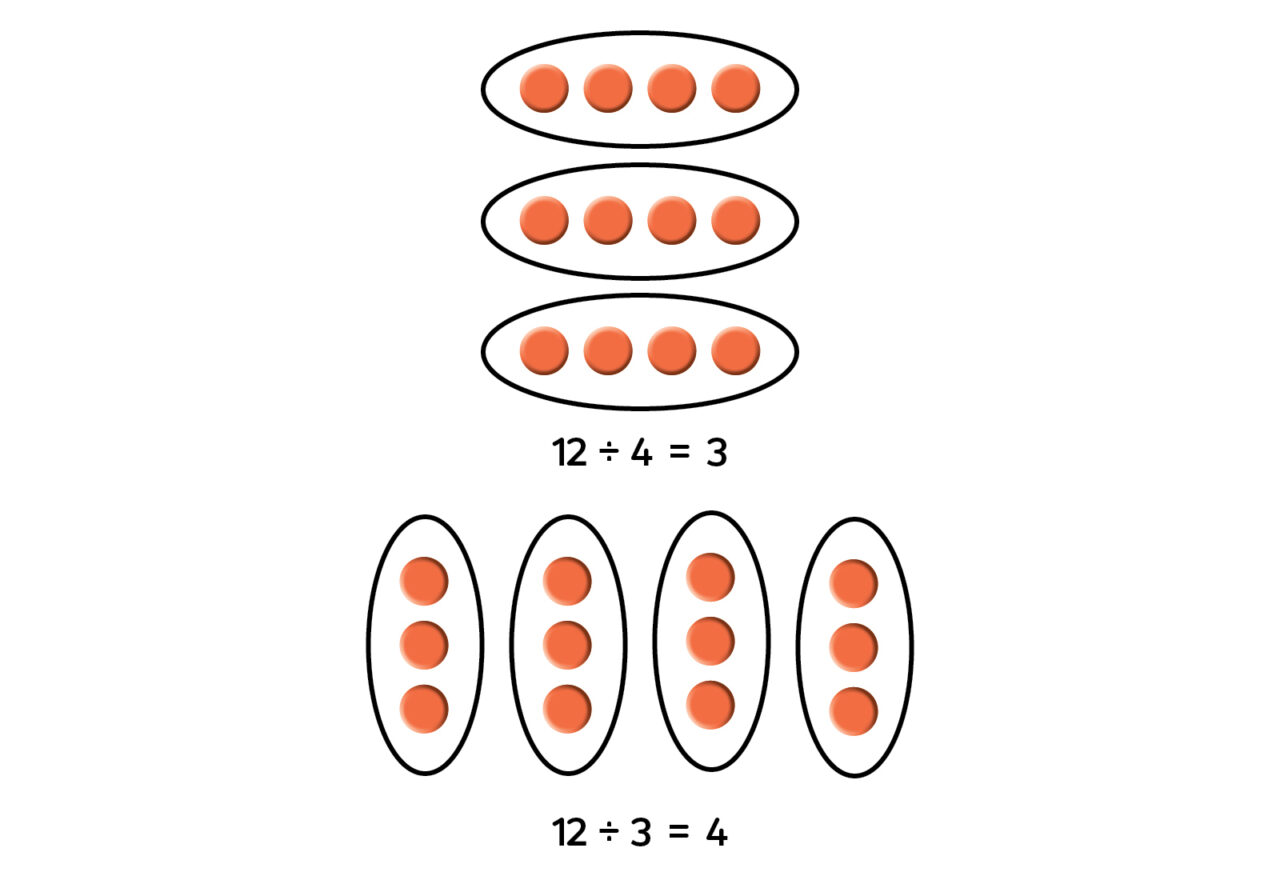
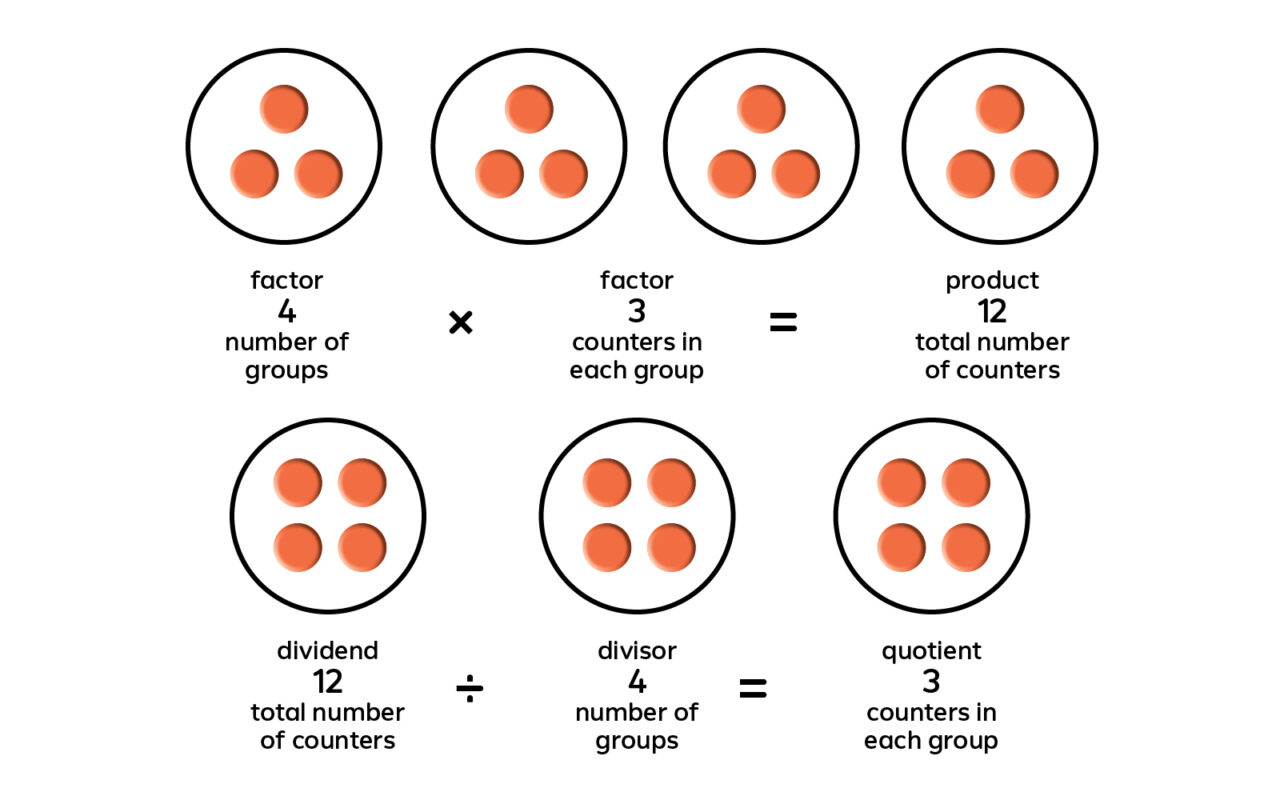
Division is the inverse, or “opposite,” of multiplication. Arrays can help students understand this relationship between multiplication and division. Multiplying involves finding the product of two factors, whereas dividing can be thought of as finding the missing factor when the product and other factor are known.
In the multiplication model below, multiplication represents finding the total number of counters. Using an array division model, division represents finding the number of counters in each group. The same three numbers are used. The model shows how division “undoes” multiplication and multiplication “undoes” division. So when multiplying or dividing, students can use a fact from the inverse operation. For example, if students know that 4 × 5 = 20, they also know the related division facts 20 ÷ 4 = 5 and 20 ÷ 5 = 4. Students can also check their work by using the inverse operation.
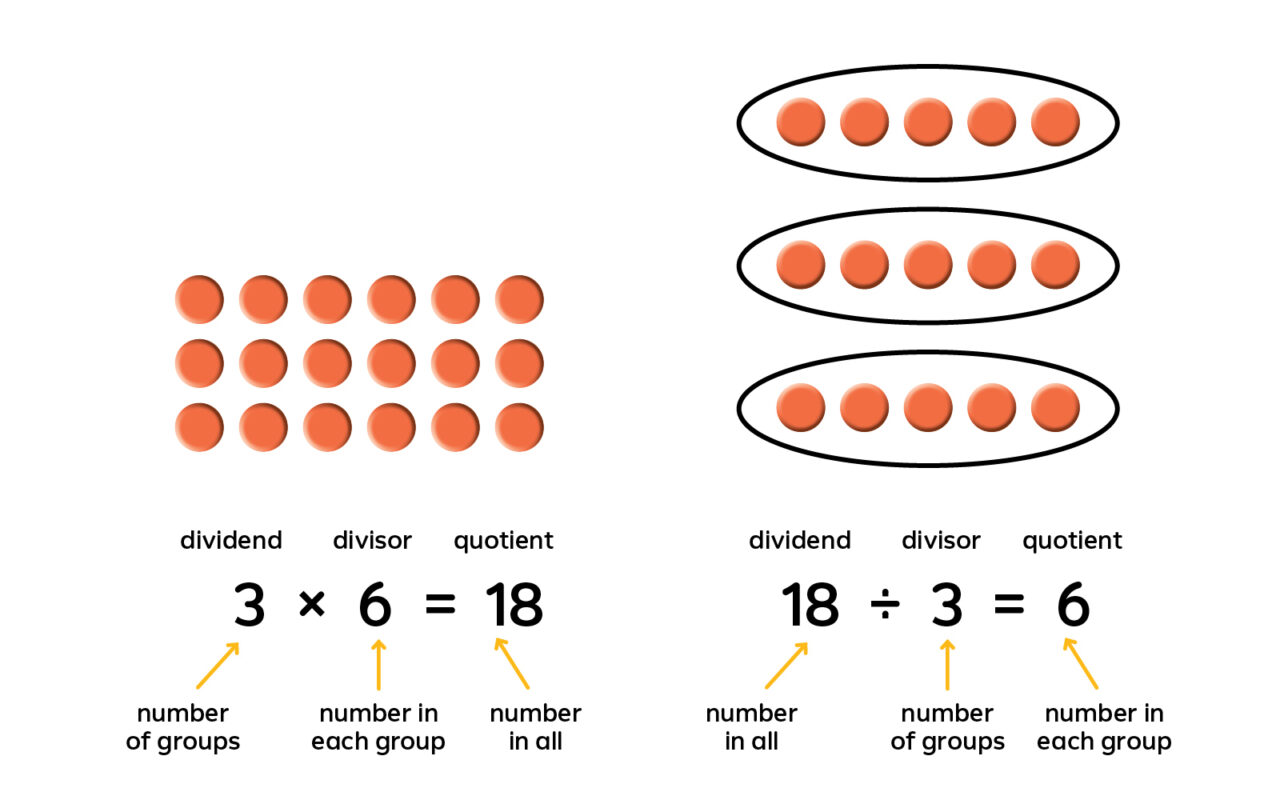
Relating multiplication and division
The numbers in multiplication and division sentences have special names. With multiplication, the numbers being multiplied are called factors, and the result of the multiplication is called the product. With division, the number being divided is the dividend, the number that divides it is the divisor, and the result of the division is the quotient. Discuss this vocabulary with your students. Not only are multiplication and division related, but the terms used to describe them are related, too.
There are other models besides arrays your students can use to explore the relationship between multiplication and division. Expose your students to the different models and let them explore which ones they find most helpful. Here is an example using counters to multiply and divide.
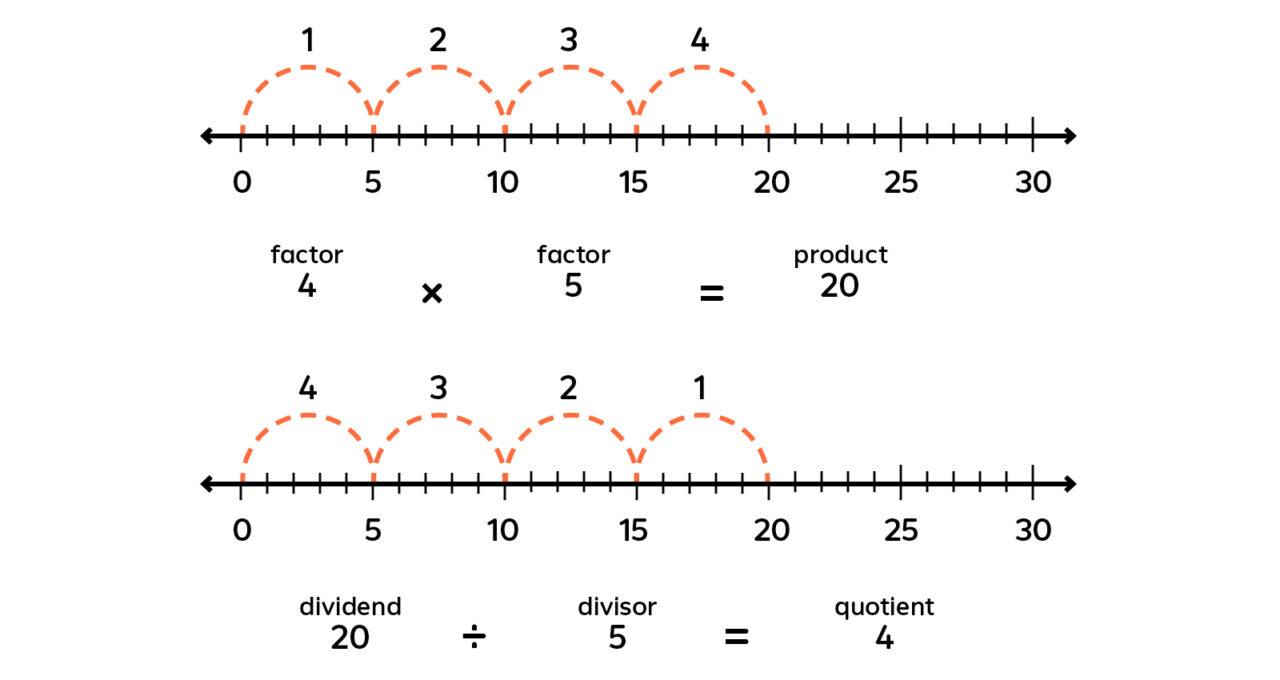
Here’s another way to model multiplication and division, this time using a number line.
Another strategy your students may find helpful is using related facts. Consider this division problem as an example:
18 ÷ 6 = ?
Students can think about the division problem as multiplication: 6 × ? = 18, or in other words, six times what number is 18? If they know the math fact that 6 × 3 = 18, then they solve the original division problem: 18 ÷ 6 = 3.
Dividing with 0 and 1
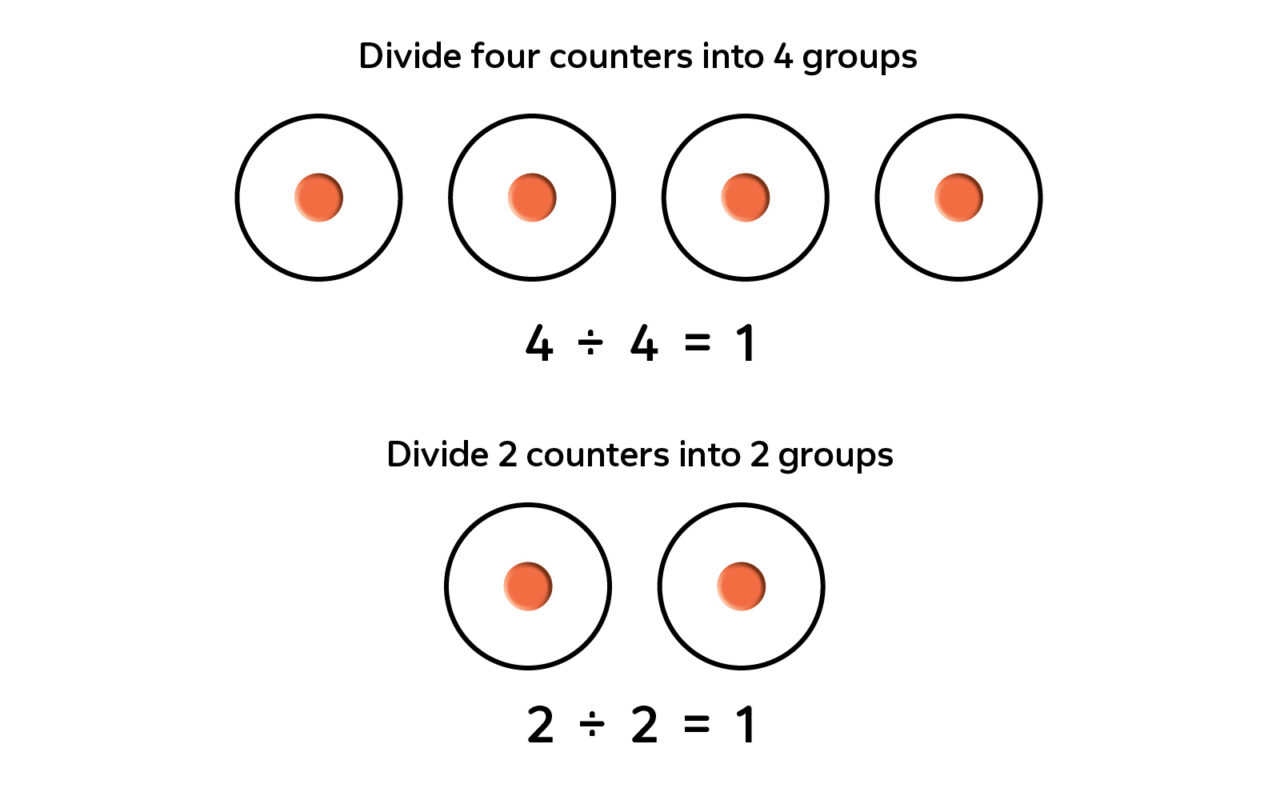
When students understand the concept of division, they can proceed to explore the rules for dividing with 0 and 1. Lead students to discover the rules themselves by having them use counters to model the division. A few examples follow.
Rule: When any number (except 0) is divided by itself, the quotient is 1.
Rule: When any number is divided by 1, the quotient is that number.
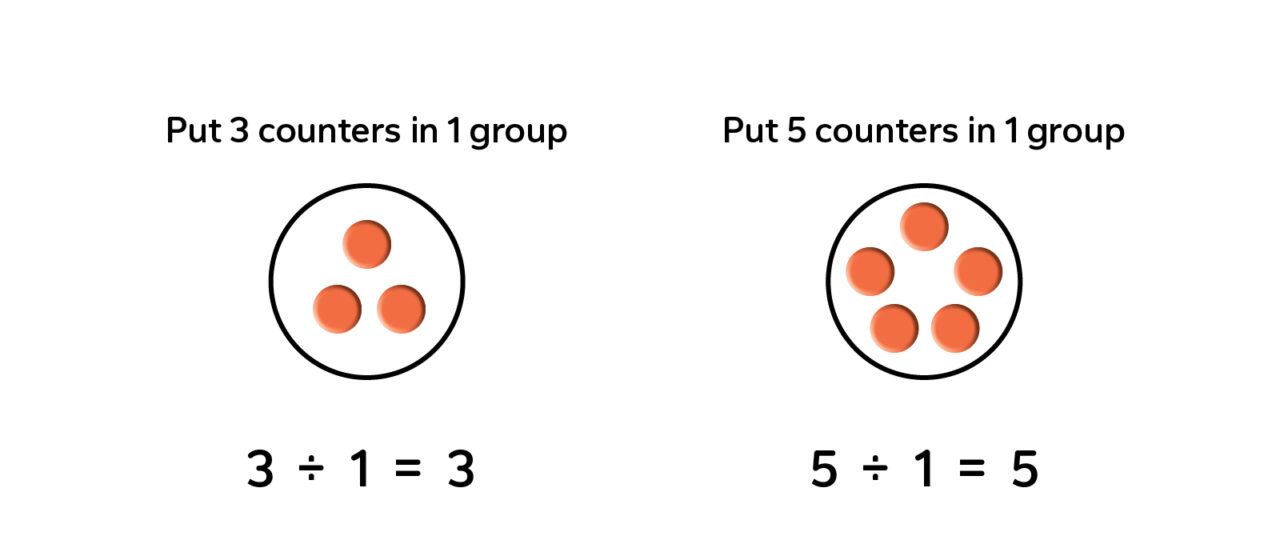
Rule: When 0 is divided by any number (except 0), the quotient is 0.
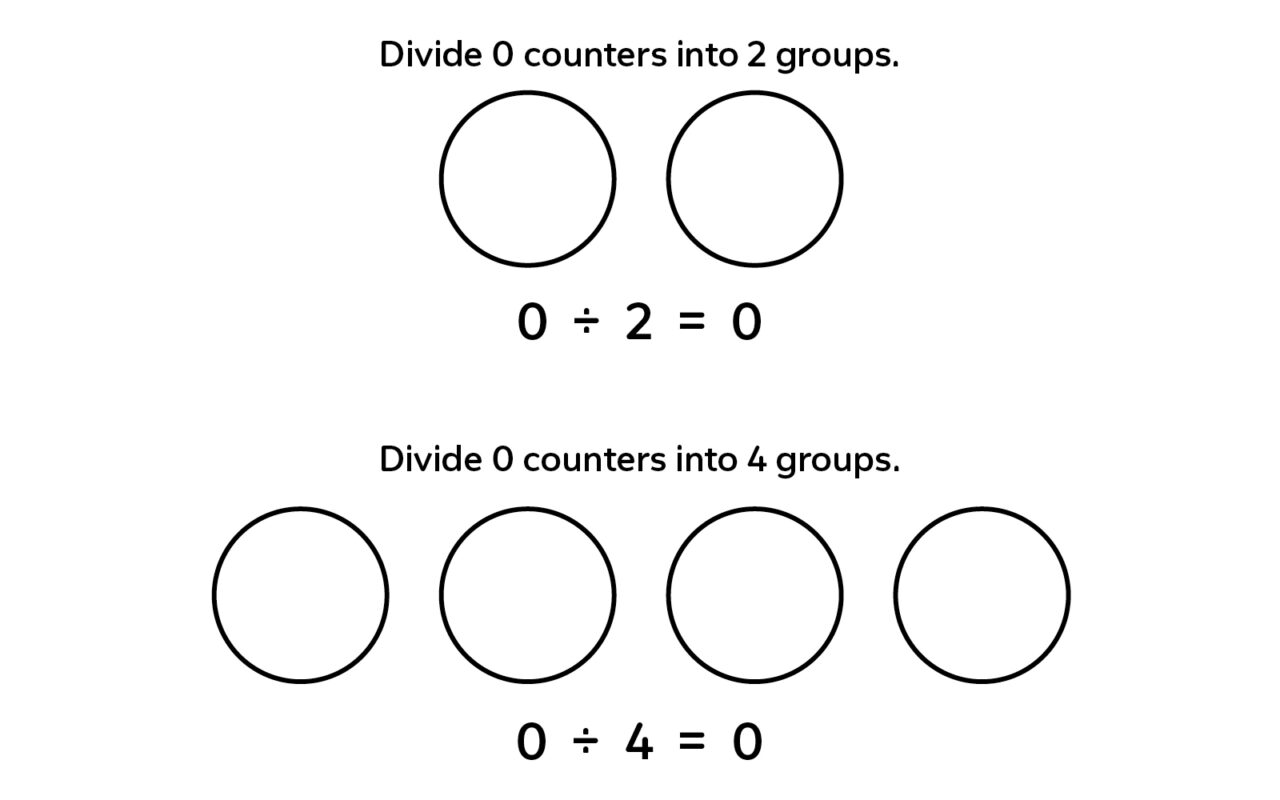
This leads to a question that continues to confound students and many teachers alike! What happens when you divide by 0? If students ask, you can explain that it is not an easy concept. When you think about it, you quickly run into paradoxes. How can you divide a number into groups so that there are zero objects in each group?! No matter how many groups you make, it doesn’t work.
For now, it works to simply say that you can’t divide by 0 or that the quotient doesn’t exist. However, in calculus and beyond, this idea is investigated more rigorously, and students learn more advanced and nuanced ways of thinking about division by zero.

Division in the real world
Encourage students to think about the relationship between multiplication and division when they solve real-world problems. One example could be when prices are given for buying more than one of an item, such as baseball caps priced at 3 for $18. Figuring out the cost for one cap is a division problem ($18 ÷ 3 = ?) that can also be thought of as a multiplication problem (3 × ? = $18).
In this example, 3 × $6 = $18, so $18 ÷ 3 = $6. The cost is $6 for one baseball cap.
***
This blog, originally published in 2020, has been updated for 2025.
Looking for more support with the question, “How are multiplication and division related?” Explore Math 180, our revolutionary approach to math intervention for Grades 3–12.
Get our free Math Intervention eBook today.














